Section 1.1 : Review : Functions
28. Find the domain of \(\displaystyle P\left( t \right) = \frac{{5t + 1}}{{\sqrt {{t^3} - {t^2} - 8t} }}\).
Show All Steps Hide All Steps
In this case we need to avoid square roots of negative numbers and because the square root is in the denominator we’ll also need to avoid division by zero issues. We can satisfy both needs by requiring,
\[{t^3} - {t^2} - 8t = t\left( {{t^2} - t - 8} \right) > 0\]Note that there is nothing wrong with the square root of zero, but we know that the square root of zero is zero and so if we require that the polynomial under the root is strictly positive we’ll know that we won’t have square roots of negative numbers and we’ll avoid division by zero.
Now, despite the fact that we need to avoid where the polynomial is zero we know that it will only change signs if it goes through zero and so we’ll next need to determine where the polynomial is zero.
Clearly one value is \(t = 0\) and because the quadratic does not factor we can use the quadratic formula on it to get the following two additional points.
\[\begin{align*}t & = \frac{{1 \pm \sqrt {{{\left( { - 1} \right)}^2} - 4\left( 1 \right)\left( { - 8} \right)} }}{2} = \frac{{1 \pm \sqrt {33} }}{2} & \hspace{0.25in}\hspace{0.25in} & t = \frac{{1 + \sqrt {33} }}{2} = 3.372281\\ & & \hspace{0.25in}\hspace{0.25in} & t = \frac{{1 - \sqrt {33} }}{2} = - 2.372281\end{align*}\]So, these three points (\(t = 0\), \(t = - 2.372281\) and \(t = 3.372281\) are the only places that the polynomial under the root can change sign.
Here is a number line giving the value/sign of the polynomial at a test point in each of the region defined by these three points. To make it a little easier to read the number line let’s define the polynomial under the radical to be,
\[R\left( t \right) = {t^3} - {t^2} - 8t = t\left( {{t^2} - t - 8} \right) > 0\]Now, here is the number line,
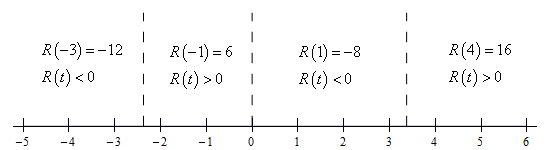
The domain will then be all the points where the polynomial under the root is positive, but not zero as we also need to avoid division by zero, and so the domain is,
\[{\rm{Domain : }}\frac{{1 - \sqrt {33} }}{2} < t < 0,\,\,\,\frac{{1 + \sqrt {33} }}{2} < t < \infty \]